Presten Thomas Bayes og medisinske beslutninger
Michael 2011;8: 189–199.
Thomas Bayes (1702–61) var prest. Han etterlot seg matematiske og statistiske arbeider som har fått stor betydning for medisinsk beslutningsdannelse. Hans arbeid har spesiell relevans for medisinsk diagnostikk, screening og forskning. Bayes teorem viser hvordan en medisinsk undersøkelse eller tests evne til å bekrefte eller avkrefte sykdom avhenger av forekomsten av sykdommen, testens evne til å fange opp de med sykdom (sensitivitet) og avkrefte sykdom hos de friske (spesifisitet). Mange medisinske feilslutninger skyldes at man ikke fullt ut benytter denne kunnskapen. Bayesianske resonnementer har også stor relevans for tolkning av forskningsresultater. Ved kunnskapsoppsummeringer samles forskningsresultater fra ulike studier som er gjennomført på forskjellige tidspunkt. Ifølge bayesiansk statistikk vil resultatene fra hver av de tidligere studiene påvirke nullhypotesene for de påfølgende studiene. Dette er forhold som det vanligvis ikke tas hensyn til i kunnskapsoppsummeringene. Det kan føre til at vi enten overvurderer eller undervurderer forskningsfunnene. Vi må anta at bayesiansk metode vil få større plass i design og analyse av randomiserte kontrollerte studier i fremtiden.
Thomas Bayes (1702–61) vokste opp rett utenfor London og var eldst av sju søsken (1). Faren, Joshua Bayes (1671–1746), var blant de seks første ikke-konforme prestene* Nonconformist minister: Those refusing to conform with the authorized formularies and rites of the Established Church of England. . www.newadvent.org/cathen/11095b. htm, 03.02.2011. 1 som ble ordinert i England etter at den engelske kirke ble etablert. Det var nok ikke et helt enkelt liv. Den engelske kirken var hardhendt med sine dissidenter. Thomas fulgte i farens spor. Ikkekonformister måtte ut av England for å studere teologi. Han ble matrikulert ved Universitetet i Edinburgh i 1719, og skrev sin valgte hovedoppgave
(homely) i 1721 over Matteus kapittel 7, vers 24–27, som omhandler avslutningen av Jesu bergpreken (2).

Thomas Bayes (1702–61)
24. Derfor, hver den som hører disse mine ord og gjør efter dem, han blir lik en forstandig mann, som bygget sitt hus på fjell;
25. og skyllregnet falt, og flommen kom, og vindene blåste og slo imot dette hus, men det falt ikke; for det var grunnlagt på fjell.
26. Og hver den som hører disse mine ord og ikke gjør efter dem, han blir lik en uforstandig mann, som bygget sitt hus på sand;
27. og skyllregnet falt, og flommen kom, og vindene blåste og slo imot dette hus, og det falt, og dets fall var stort (3)
Allerede som 19-åring hadde han staket ut kursen. Thomas ville være en forstandig mann. Han ville bygge sin kunnskapsbase på fjell, ikke på sand. Og det var det han gjorde. Thomas Bayes ble ordinert som ikkekonform prest som sin far, og tjenestegjorde som presbytariansk prest først i Holborn nord i London, og deretter ved Presbytarian Chapel litt sørvest for byen.
Selv om han ble vennlig omtalt som prest, er det som matematiker han blir husket. Hele yrkeslivet tjente han sin kirke, og de færreste i menigheten var nok klar over hans matematiske genialitet. Under et pseudonym publiserte han enkelte matematiske arbeider mens han levde. Det gav ham medlemsskap som Fellow of the Royal Society fra 1742. Men hans sannsynlighetsteori «Essay towards solving a problem in the doctrine of chances» ble publisert først to år etter hans død. Langsomt ble arbeidene hans anerkjent i vitenskapelige kretser. Den franske matematikeren Pierre-Simon Laplace (1749–1827), kjent for bevisene for solsystemets stabilitet, skrev om det unike arbeidet i sine memoarer fra 1781 (2). Thomas Bayes etterlot seg en unik notatblokk, som inneholder betydelige matematiske arbeider, inkludert diskusjoner om sannsynlighet, trigonometri, geometri, ligningsløsninger, serier og differensialregning. I notatblokken drøfter han også temaer som elektrisitet, optikk og himmellegemer (4).
Kanskje forsto han heller ikke selv hvor praktisk viktig hans arbeider skulle bli, blant annet innenfor medisinen. Han visste nok heller ikke at statistikere og forskere over 250 år senere fremdeles søker etter nye områder hvor teoriene hans får stor betydning.
Legens diagnostiske resonnement
En pasient som går til legen med ønske om hjelp, presenterer en sykehistorie, en fortelling, opplevelser med smerter, nedsatt funksjonsevne eller andre tegn på sykdom eller lidelse. Umiddelbart starter et avansert forståelsesløp. Pasienten og legen samarbeider om å finne ut hva slags fenomen tilstanden representerer, om det er sykdom eller normaltilstand, om tilstanden er godartet, om den vil lege seg selv, om det finnes effektiv behandling mot den, om pasienten selv kan gjøre noe for å bli kvitt den eller forebygge forverring. Den kliniske tenkningen i medisinen er spennende og sammensatt. Gjennom sin utdannelse og erfaring har legen lært å kjenne igjen visse mønstre som peker i retning av spesifikke sykdomsbilder. Forståelsesprosessen kompliseres ytterligere ved at skillet mellom syk-frisk og uhelse-helse ikke er konstant gjennom historien og på tvers av kulturer.
Helt fra medisinens første tid har man lett etter logiske sammenhenger eller spesielle tegn som indikerer at pasienten kan være syk. Det er avgjørende at legen klarer å forstå at pasienten er syk hvis hun virkelig er det. En lege som ikke klarer å finne ut hvem som er syk og hvem som er frisk, er ikke spesielt verdifull for pasienten. Unntaket må være hvis det ikke finnes be-handling mot sykdommen. Naturligvis kan legen både være omsorgsfull og god på bunnen som vi sier. Vi krever likevel mer av den profesjonelle legen enn omsorg og godhet. Derfor vil legen forsøke å utstyre seg med et forståelsesapparat som er sensitivt nok i forhold til å fange opp de som faktisk er syke. Nedsatt allmenntilstand, ufrivillig vekttap, sterke smerter, feber, nedsatt funksjonsevne er eksempler på forhold som indikerer sykdom. Men noen er syke selv om de ikke presenterer slike symptomer og tegn, og en del av de som kommer med slike plager, er ikke nødvendigvis syke.
Ved siden av å lete etter generelle sykdomstegn som gjør at vi fanger opp de som er syke, leter vi også etter spesifikke sykdomstegn. Hvis det spesifikke sykdomstegnet er til stede, vet vi med stor sikkerhet at pasienten faktisk har en bestemt sykdom eller lidelse. Det enkleste er kanskje det man umiddelbart kan se. Ved mange infeksjonssykdommer med hudutslett, som meslinger, vannkopper og røde hunder forekommer slike spesifikke sykdomstegn. Den gode klinikeren ser forskjell på hudutslettene, iallfall når de er typiske. Har man typiske vannkopper, feiler man ikke noe annet. Ved en rekke andre sykdommer som hudlidelser, leddgikt, hjerneslag og nevrologiske lidelser finnes også slike spesifikke tegn. Gjennom hele den kliniske undersøkelsen hvor legen bruker alle sine sanser som syn, hørsel (auskultasjon), lukt, berøring (varme-kulde, motstand-mykhet), palpering og banking, leter klinikeren etter mønstre som bidrer til at vi fanger opp den som er syk og avkrefter sykdom hos den friske.
I forståelsesprosessen frem mot diagnosen forsøker klinikeren bevisst eller ubevisst å utnytte slik sensitiv og spesifikk informasjon. På bakgrunn av kunnskap, erfaring og skjønn gjør legen en vurdering og faller ned på en foreløpig konklusjon. Disse foreløpige konklusjonene kan grupperes i tre:
Det er mest trolig at pasienten er frisk
Det er mest trolig at pasienten er syk, men usikkert hva hun feiler
Det er mest trolig at pasienten er syk og legen antar det er denne spesielle tilstanden
Verken pasienten eller legen ønsker å bli værende i det andre alternativet. Det er naturligvis avgjørende at beslutningene er så sikre som mulig. Utsagn som «jeg tror aller helst du er frisk, men det er nesten like trolig at du er syk», er neppe en slager på legekontoret.
Bayes’ teorem i diagnostikken
Bayes’ teorem danner grunnlaget for slike logiske beslutningsprosesser i diagnostikk. Kjernebudskapet er at sannsynligheten for en hendelse A gitt en hendelse B (f. eks. sannsynligheten for at en kvinne har brystkreft gitt at hun har testet positiv på mammografi) ikke bare er avhengig av forholdet mellom hendelsene A og B (dvs. mammografiens treffsikkerhet), men også av førsannsynligheten (forekomsten av brystkreft i den aktuelle befolkningen) for hver hendelse.
Det enkle matematiske uttrykket for Bayes’ teorem er dette (5):
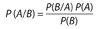
I vårt eksempel kan vi bruke følgende forklaringer:
P(A/B) er den betingete sannsynligheten for brystkreft etter at vi vet svaret på mammografien. Det er dette vi ønsker svar på.
P(A) er sannsynligheten for brystkreft før vi tar mammografi, dvs. a priori forekomst av brystkreft i befolkningen
P(B/A) er den betingete sannsynligheten for positivt mammografisvar gitt brystkreft (sanne positive), dvs, testens sensitivitet
P(B) er sannsynligheten for et positivt mammografisvar blant alle som tar prøven.
La oss ta et annet eksempel. En 50 år gammel mann kommer til legen etter en måned med tilbakevendende smerter i brystet i forbindelse med anstrengelse. En av sykdommene legen må tenke på er koronar hjertesykdom. Det kan naturligvis være en rekke andre tilstander, men la oss for enkelhets skyld følge tenkningen i forhold til denne ene sykdommen. Legen vil på basis av kunnskap om forekomst av sykdommen for menn i denne aldersgruppen danne seg et første bilde av sannsynligheten for at denne pasienten har koronarsykdom. Bayes ville kalt dette «førsannsynlighet» (a priori sannsynlighet). Deretter ville han tatt for seg en etter en av de relevante opplysningene i sykehistorien. Hvor pasienten bor, hvilket yrke han har, om han røyker, har diabetes, hvordan smertene beskrives, hvordan de kan utløses osv. Etter hvert kan vi legge på diagnostiske tester, slik som elektrokardiogram, ulike blodprøver, evt. belastningstester av hjertet og spesielle røntgenundersøkelser. Hver og en av disse opplysningene gir ny informasjon som avhengig av utfallet enten styrker eller svekker antakelsen om at vår pasient har koronarsykdom. Bayes ville sagt at sannsynligheten for sykdom etter denne tilleggsinformasjonen er en betinget (conditional) sannsynlighet.
Sensitivitet, spesifisitet og 2x2-tabellen
Innen medisinsk diagnostikk er målet høy presisjon. Derfor ønsker vi å vite hvor gode undersøkelsene vi utfører, er til å bekrefte eller avkrefte sykdom. En test som er svært god til å fange opp alle de som er syke sier vi har høy sensitivitet. En test som er svært god til å avkrefte sykdom, dvs. å bekrefte at du er frisk hvis du faktisk er det, sier vi har høy spesifisitet. I en slik enkel modell kan vi ha fire utfall. Testen kan være sant positiv (pasienten er syk og testen viser at pasienten er syk), testen kan være falskt positiv (pasienten er syk, men testen er negativ), testen kan være sant negativ (pasienten er frisk og testen viser at pasienten er frisk) eller testen kan være falskt negativ (pasienten er syk, men testen viser at pasienten er frisk). Testens sensitivitet er derfor knyttet til i hvor stor grad den er sant positiv, og testens spesifisitet til i hvor stor grad den er sant negativ.
Det er to viktige apsekter knyttet til å bruke Bayes’ teorem i medisinsk diagnostikk som stadig resulterer i diagnostiske feilslutninger. For det første vil testens evne til å bekrefte eller avkrefte sykdom avhenge av det Bayes kalte førsannsynlighet. Mange unge leger som har fått utdannelsen ved store sykehus hvor forekomsten av sjeldne sykdommer er ganske stor, tar med seg denne erfaringsbakgrunnen når de begynner å arbeide i primærhelsetjenesten. Da er mulighetene til stede for at de overvurderer sannsynligheten for en rekke lidelser. Det er avgjørende å forstå at førsannsynligheten (forekomsten) varierer betraktelig avhengig av hvor man arbeider i helsetjenesten. Symptomet hodepine har f. eks. en helt annen informasjonsverdi hos en pasient på nevrologisk avdeling ved et universitetssykehus enn tilsvarende symptomer på venteværelset hos primærlegen. Kanskje er det 100 ganger mer sannsynlig at pasienten som er henvist til nevrologisk avdeling, har en alvorlig hjernesykdom enn pasienten som sitter med tilsvarende hodepine på venteværelset hos primærlegen. Det skyldes naturligvis at man hos pasienten som utredes ved nevrologisk avdeling allerede har utelukket en rekke mindre alvorlige årsaker som ikke hadde ført til henvisning til sykehus.
Det andre forholdet er testens prediktive egenskaper, dvs. dens sensitivitet (evne til å fange opp de syke) og spesifisitet (evnen til å fange opp/ ekskludere de friske). Det er oppsiktsvekkende hvor ofte leger overvurderer testers prediktive egenskaper. Det gjelder både i diagnostikk og screening. Enda vanskeligere blir dette for den øvrige befolkningen, som ofte vil ha en stor tiltro til medisinske undersøkelser. Ved flere screeningundersøkelser som benyttes i primærhelsetjenesten, slik som screening for brystkreft, prostatakreft, kolonkreft eller livmorhalskreft, vil det være omtrent like vanlig å være frisk som å være syk selv om man har positive funn.
Det finnes praktisk talt ingen tester som er 100 % sensitive og 100 % spesifikke i forhold til sykdom. Svært gode tester kan ha sensitivitet og spesifisitet på over 95 %, mens mange tester vi bruker kanskje har en sensitivitet og spesifisitet på mellom 50 og 80 %.
Der hvor testen har en trinnvis eller kontinuerlig skala, kan vi ved å endre innslagsnivå for hva som er positivt og negativt, også endre sensitivitet og spesifisitet. Et eksempel kan være kroppstemperatur ved influensa. Under influensapandemien (2009–10) ble det fortalt at et typisk kjennetegn ved influensa var temperatur over 39,5 gr C. Det finnes åpenbart mange med influensa som ikke vil ha så høy kroppstemperatur. Ved å sette grensen til 37,5 gr C ville man kanskje fange opp nesten alle de med influensa (sensitiviteten ville være høy), men på den annen side ville et stort flertall av de som hadde temperatur over 37,5 gr C enten være helt friske eller ha helt andre sykdommer (spesifisiteten ville være lav).
I eksempelet nedenfor (tabell 1) tenker vi oss at vi tester 1000 pasienter med tanke på en spesiell sykdom. Forekomsten av sykdom er 10 % i denne pasientpopulasjonen og testen som skal gi oss ytterligere informasjon om hvem som er frisk og hvem som er syk har en sensitivitet og spesifisitet på 90 %:
Syk |
Frisk |
Totalt |
|
Test positiv |
90 |
90 |
180 |
Test negativ |
10 |
810 |
820 |
Totalt |
100 |
900 |
1000 |
I dette eksempelet ser vi at 90 er sant positive, 90 er falskt positive, 10 er falskt negative og 810 er sant negative. Vi ser at sannsynligheten for sykdom gitt at testen er positiv er 50 %.
Dess sjeldnere sykdommen er, dess forsiktigere bør helsetjenesten være med å ta unødvendige undersøkelser. La oss se på hva som skjer hvis forekomsten av sykdom er bare 1 % og sensitivitet og spesifisitet fortsatt er 90 % (tabell 2):
Syk |
Frisk |
Totalt |
|
Test positiv |
9 |
99 |
108 |
Test negativ |
1 |
891 |
892 |
Totalt |
10 |
990 |
1000 |
I denne situasjonen vil bare 9 av 108 som har positiv test være syke, dvs. 8 %. Derimot vil andelen falskt negative være liten, dvs. nær 0,1 %.
Det er på denne måten lett å vise at når førsannsynligheten er så lav som 1 %, må sensitiviteten og spesifisiteten til prøven være over 99 % for at det skal være mer enn 50 % sannsynlig at pasienten er syk ved positivt prøvesvar (tabell 3) .
Syk |
Frisk |
Totalt |
|
Test positiv |
10 |
10 |
20 |
Test negativ |
0 |
980 |
980 |
Totalt |
10 |
990 |
1000 |
Bayesiansk statistikk i forskning
I den senere tid har statistikere drøftet betydningen av bayesiansk tenkning også i forskning (6). Mange kunnskapsoppsummeringer baserer seg på en systematisk sammenstilling av funn i flere studier. Når man sammenstiller informasjonen fra de ulike studiene, f. eks. randomiserte kontrollerte studier (RCTer), legges informasjon fra studier som er gjennomført over ulike tidsintervall sammen.
I en slik metaanalyse ønsker man å teste ut en hypotese (nullhypotese). Det handler derfor om sannsynligheten for et datasett (den samlede informasjonen man har) gitt en spesifikk hypotese, vanligvis nullhypotesen. Nullhypotesen er vanligvis at det fenomenet (f. eks. en behandling eller et tiltak) som studeres, ikke gir andre eller bedre resultater enn det man sammenligner med. Gjennom metaanalysen, hvor mange studier inkluderes, kan antallet individer som er inkludert i analysen bli større, et forhold som reduserer usikkerheten i funnene.
En bayesianer kan innvende at vi sjelden starter med en hypotese om at fenomenet ikke har effekt, eller at det ikke er forskjell mellom gruppene. Førsannsynligheten er sjelden null. Det kan være gjennomført andre studer, kvalitative eller observasjonelle, eller tidligere små randomiserte studier som bør påvirke nullhypotesen. Den kan bli mer sannsynlig, eller mindre sannsynlig enn null. Er det ikke da riktig å trekke denne førsannsynligheten inn i vurderingen?
The GREAT trial (7) var laget for å teste hypotesen om at tidlig trombolyse som blir gitt av legevaktslegen i hjemmet ville være bedre enn senere behandling
i sykehuset. Forskerne gjennomførte en RCT som sammenlignet de to behandlingsregimene. Etter tre måneder var den relative reduk sjonen i total letalitet 49 % (p=0,04) for pasienter behandlet hjemme sammenlighet med de som fikk behandling i sykehus. Funnet syntes nesten utrolig, gitt at det var dokumentert at sykehustrombolyse i seg selv reduserer dødeligheten med omkring 25 %.
Pocock & Spiegelhalter (8) foretok en bayesians reanalyse av materialet. De pekte på at førsannsynligheten ikke var null reduksjon i letalitet, basert på tidligere studier. Forfatterne mente å kunne vise at førsannsyligheten hadde en fordeling som er vist i den øverste figuren (A). Forfatterne viste at den forventede effekten basert på tidligere studier (førsannsynligheten) var 15–20 %, men med en betydelig usikkerhet i det forventede resultatet. Basert på funnene i undersøkelsen (B), som altså anga en 49 % reduksjon i letalitet, kunne de da estimere sannsynlighetsfordelingen for at tidlig trombolyse i hjemmet ga bedre resultater (C). Konklusjonen var at reduksjonen i tre måneders letalitet neppe var 49 %, men sannsynligvis mellom 20 og 30 % (den nederste figuren), men med en usikkerhet som strekker seg fra svært liten effekt til opp mot 40 %. Både at effekten skulle være større enn 40 % og at det ikke var effekt i det hele tatt var svært usannsynlig. I figurene ser vi at Pocock & Spiegelhalter tar hensyn til både forventningsverdier og spredningsmål. Hvis vi studerer fordelingene i figur A-C, ser vi at den aktuelle studien (B) har bidratt til to forhold. For det første har den forventede effekten av tiltaket blitt større (forflytning på x-aksen fra figur A til C). For det andre har usikkerheten rundt forventningsmålet blitt mindre (mindre spredning i figur C enn A).
I en interessant artikkel i The Lancet i 2008 skriver professor emeritus Michael Rawlins ved NICE at det kan være fem hovedgrunner til at bayesianske metoder ikke blir brukt oftere i forskningen (6):
For det første ser en del forskere med skepsis på den subjektive tilnærmingen som det å etablere en fordeling av en førsannsynlighet innebærer. Det til tross for at det i mange situasjoner er illusorisk at det ikke finnes. Det er vanligvis mulig å estimere en førsannsynlighet som er riktigere enn det standpunktet at man ikke har noe kunnskap.
For det andre er det uenighet om hvordan man beregner førsannsynligheten. Den enkleste situasjonen har vi når det finnes tidligere studier. Det er vanskeligere når vi ikke har tidligere studier å bygge på, og man anvender det som kalles forhåndsvalgte (default) sannsynligheter basert på skjønn.
For det tredje er bayesianske analyser ganske komplekse og krevende.
For det fjerde mangler en del statistikere og forskere kunnskap om bayesiansk analyse og er lite villige til å tilegne seg denne kunnskapen.
Sist, men ikke minst, har myndighetene som vurderer medisinsk teknologi i liten grad tatt i bruk bayesiansk tenkning i sitt regelverk (9).
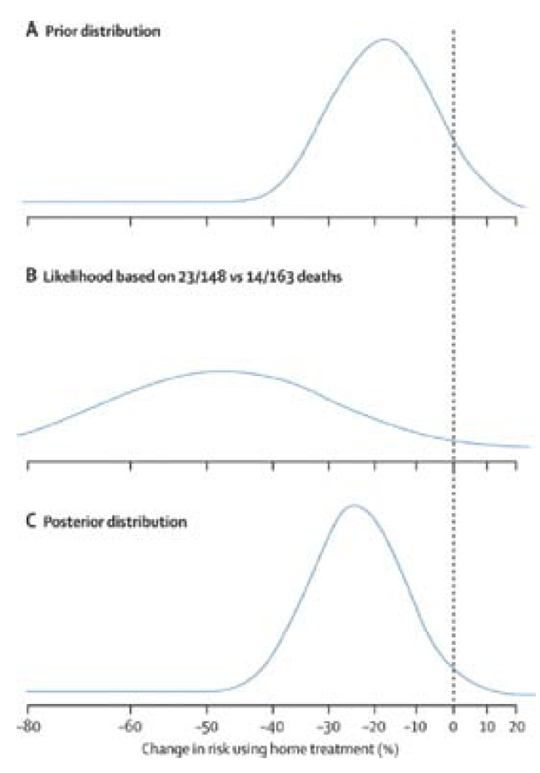
Figur 1. Bayesiansk reanalyse av The GREAT trial (7) som viser dødelighetsreduksjon ved trombolytisk behandling i hjemmet sammenliknet med trombolyse i sykehus.
Når vi ikke bruker bayesiansk metode i forskningen, kan vi lett komme til å treffe feilaktige slutninger. Vi kan både komme til å overvurdere og undervurdere betydningen av ny forskning.
Vi må anta at bayesiansk metode vil få langt større plass i design og analyse av randomiserte kontrollerte studier i fremtiden. Det vil være av stor verdi å frigjøre seg fra begrensningene som fikserte p-verdier representerer. Fremfor alt vil bayesianske tilnærminger hjelpe beslutningstakere å trekke bedre og riktigere konklusjoner.
Litteratur
Hacking I. Biography. I: Dictionary of Scientific Biography. New York: Gale, 1970–1990.
The MacTutor History of Mathematics archive. www-groups.dcs.st-and.ac.uk/~history/ Biographies/Bayes.html (11.02.2011)
Bibelen. Revidert oversettelse av 1930. Oslo: Det norske bibelselskaps forlag, 1973.
Dale AI. Most Honourable Remembrance : The life and work of Thomas Bayes. New York- Berlin- Heidelberg: Springer, 2003.
Weinstein MC, Fineberg HV et al. Clinical decision analysis. London: WB Saunders,1980.
Rawlins M. De testimonio: on the evidence for decisions about the use of therapeutic interventions. Lancet 2008;372: 2152–61.
GREAT Group. Feasibility, safety, and efficacy of domiciliary thrombolysis by general practitioners: Grampian region early anistreplase trial. BMJ 1992; 305: 548–553.
Pocock SJ, Speigelhalter DJ. Grampian region early anastroplase trial. BMJ 1992; 305: 1015.
Berry D, Goodman SN, Louis TA, Temple R. Introduction to bayesian methods: floor discussion. Clin Trials 2005; 2: 301–304.
Helsedirektoratet
Postboks 7000 St. Olavs plass
0130 Oslo
bjorn.guldvog@helsedir.no
